
Метод конечных элементов представляет собой способ, который решает дифференциальные уравнения. В настоящий момент он получил теоретические обоснования, что помогло ему найти применения в решении самых разнообразных задач. Его суть состоит в том, что уравнения разбиваются до конечных подобластей или, по-другому, элементов, после чего в каждом отделе произвольно выбирают вид аппроксимирующих функций.
При этом, если функция находится за пределами своего элемента, то у нее нулевое значение. В самом простом случае, она представляет собой полином первой степени. Таким образом, любая непрерывная величина аппроксимируется в дискретную модель, к примеру:
- перемещение;
- температура;
- давление.
В ходе моделирования, построение происходит на множестве кусочно-непрерывных функций. Определяются они по конечной цифре в подобластях.
Используя матричные термины, в итоге образуются матрицы жесткости по условию Дирихле. Потом на них накладывают граничные данные. Притом стоит отличать, что при вышеобозначенных условиях, матрицы исключают определенное количество строк и столбцов, которые соответствуют узлам. Это связано с тем, что компоненты решений уже известны. Также часто используют данные условия, если есть уравнение Пуассона. Но если при составлении матриц руководствоваться условиями Неймана, то они остаются без изменений.
Задачи и методы расчета МКЭ
Область применения МКЭ достаточно широка. Во многих сферах можно найти употребление данного метода, притом его применение весьма успешно. Чаще всего система конечных элементов (МКЭ) применяется в следующих случаях:
- стационарные задачи, которые помогают определить распространение теплопередачи, диффузии или распределение электродинамики, различные задачи теории электрического поля;
- применяют в гидромеханике, например, движение жидкостей в различной среде;
- принципы в механике и прочности различных конструкций, а именно при проектировке летательных аппаратов, пространственных оболочек;
- применяется в прикладной математике, например, при решении интегральных уравнений различных типов (линейных и нелинейных). Наиболее яркий пример – это задачи Фредгольма и Вольтерра (второго рода);
- определение ползучести, жесткости и т.д. при расчете конструкций различного рода.
У данного метода, несмотря на его относительную сложность, есть ряд преимуществ, которые отлично демонстрируют себя при решении реальных задач. В частности:
- Произвольная форма для обрабатываемой сферы.
- Если не требуется высокая точность в определенных разделах, то сетки в тех местах можно сделать более редкими.
Некоторое время расчет МКЭ не пользовался особой популярностью. И связано это было с тем, что отсутствовали алгоритмы, позволяющие автоматически разбивать области без особых погрешностей в виде почти равносторонних треугольников. Однако благодаря применению триангуляции Делоне, этот недостаток быстро устранили.
Сервис для автоматизации расчетов МКЭ
Сервис представляет собой мощное программное обеспечение, которое быстро и с высокой точностью поможет провести моделирование и анализ. С его помощью можно исследовать напряженно-деформированные состояния элементов конструкции.
Также он поможет в проектировании 2D и 3D моделей, которые состоят из различных элементов. Например:
- стержней различных параметров;
- стен;
- множества плит составного типа;
- оболочек;
- элементов различной твердости.
Более того, сервис работает с учетом различных особенностей при решении задач различного типа. Например, с влиянием уравнений Пуассона.
Разные численные методы, по сравнению с МКЭ, не всегда являются столь же эффективными. Довольно популярный метод конечных разностей хоть и является проще в использовании, но уступает во множестве других возможностей. Поэтому при проектировании или решении уравнений, задач различного типа применяют именно МКЭ.
Тем более что область, в которой метод можно использовать, действительно велика. Наши клиенты применяют сервис для вычисления не только самых простых задач, но и для более сложных, например, проектировка дома, котельной, фильтров и т.д. Интуитивно простая программа делает использование действительно удобным. Оператору не требуется слишком много времени, чтобы разобраться в принципе работы.
Примеры использования сервиса
Предлагаем воспользоваться простым примером, чтобы было понятно, как работает сервис.
В первую очередь выберите тип решаемой задачи:
- изгиб тонкой пластины (прямоугольные КЭ);
- изгиб тонкой пластины (треугольные КЭ).
Приведем пример на прямоугольных пластинах.
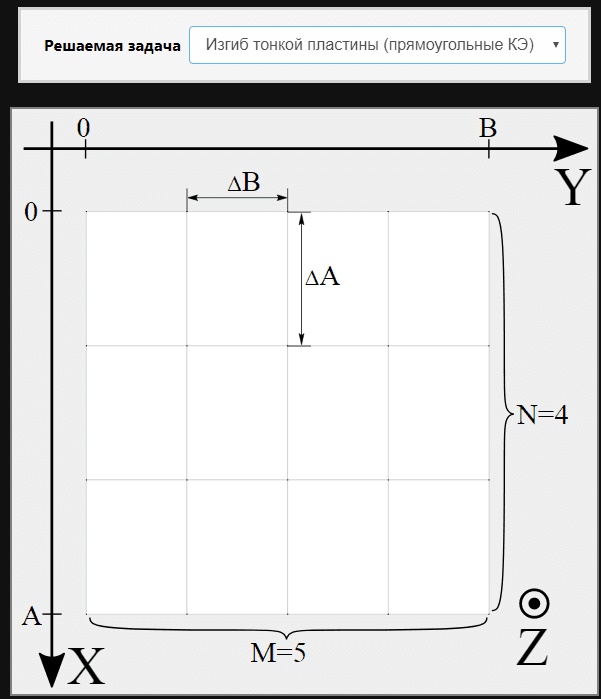
Далее вы увидите перед собой сетку, для которой нужно ввести следующие значения: ширину, длину и толщину пластины по различным осям, коэффициент Пуассона, модуль Юнга. Единицы измерения можно выбрать, исходя из ваших данных.

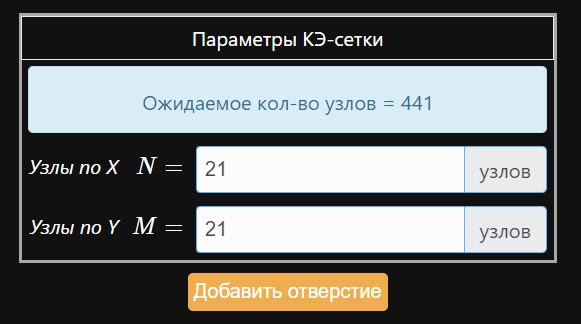
После этого задайте параметры КЭ-сетки: выберите количество узлов по различным осям. Кроме того, можно добавить отверстие при необходимости.
Далее необходимо указать способ закрепления пластины: защемление,неподвижная опора и без крепления.

На конечном этапе выберите вид нагрузки и задайте ее значение.
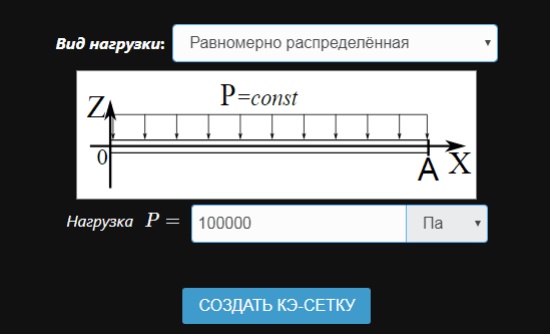
Далее нажмите кнопку "Создать КЭ-сетку".
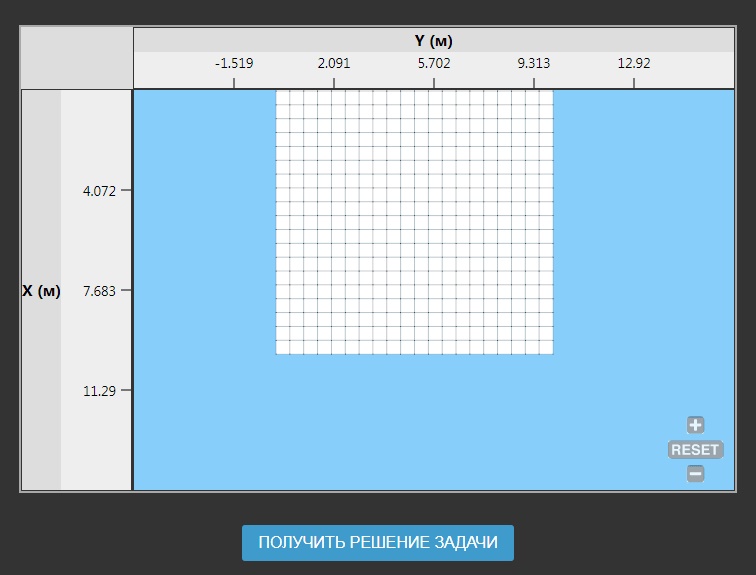
После этого остается только получить решение задачи.
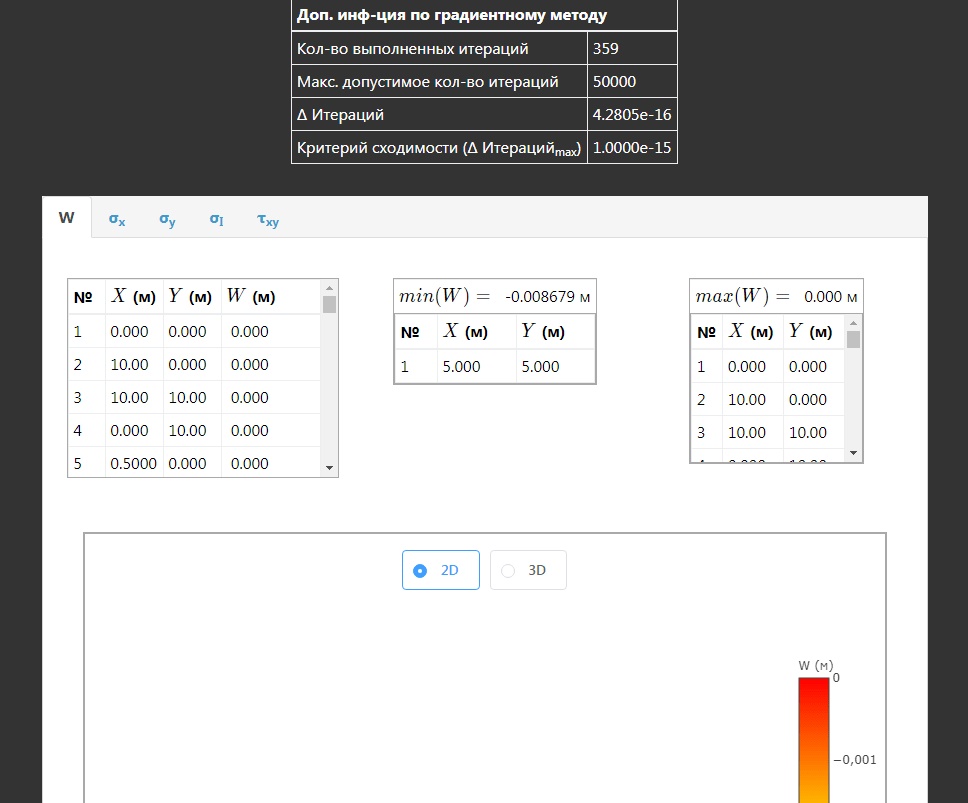
Можно выбрать различные линии сечения, которые нужно изучить. Элементы просматриваются в 2D и 3D-формате для удобства пользователя или согласно его требованиям. На этом решение задачи закончено, при этом в ходе всех вычислений программа выдает различные дополнительные данные, которые помогают лучше понять особенности уравнения.