

Сегодня доступно огромное количество методов распознавания образов для проведения диагностики тех или иных объектов. Однако наиболее точным и прогрессивным считается Байесовский подход, сейчас он получил широкую популярность и применяется в различных сферах.
Базируется он на теореме или формуле Томаса Байеса – английского математика, который проживал в XVIII веке. Его работы стали основополагающими, а после некоторых дополнений стали особенно актуальны. Теперь методы активно применяются в распознавании образов, что облегчает обработку огромного количества чисел, появляющихся при регистрации и измерении признаков исследуемых объектов. Все они составляют вектор наблюдений, который является основой формулы.
Задачи и методы распознавания, формула Байеса
Для того чтобы решить какую-либо задачу с минимальным количеством ошибок применяют системы распознавания образов, основанный на формуле Байеса. Обладая конечным списком, где указаны исторические данные об исследуемом объекте, сделать это намного проще. Такой метод является фундаментальным в результатах теории машинного обучения.
Формула относится к статистическим методам. Также, чтобы понять точнее, как именно работает принцип, нужно разобраться в основных понятиях вероятности. Притом если объем данных позволяет использовать именно данный метод, то он считается самым надежным и эффективным.
Основа заключается в том, что во время обработки данных при наличии априорных вероятностей, появление различных образов является случайным процессом. Притом описание события происходит следующим образом:
- с помощью закона распределения некоего количества вероятностей;
- используются многомерные величины, которые подаются в различной форме;
- задав элементы выборки обучения, восстанавливаются характеристики изучаемой сферы.
Также стоит заметить, что формула может использоваться для задач распознавания образов даже в случаях, когда некоторое число признаков обладает дискретным и непрерывным распределением.
Все вычисления производятся через формулу Байеса, имеющую следующий вид:
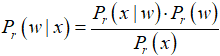
Чтобы привести задачу к такому виду, используется определение условной вероятности:
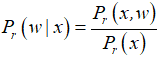
Из чего можно сделать вывод:
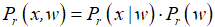
Таким образом, применив соответствующие математические методы, получается нужная формула.
В ходе распознавания объектов применяется байесовский классификатор, который в качестве основы использует наблюдаемые признаки, и во время математической реализации, относит объекты к определенному классу, используя наибольшую вероятность.
Стоит также заметить, что нейросеть предполагает эффективную постройку нелинейных зависимостей. Наборы данных куда более точно описываются в результате обработки.
Существуют также другие теории распознавания образов, однако на данный момент метод Байеса является наиболее оптимальным.
Сервис для определения признаков в обучающей выборке
Мы предоставили простую возможность вычислить нужные данные с помощью данного сервиса. Использовать программы распознавания образов достаточно легко. Пользователи фактически получают доступ к нейронной сети для нужных вычислений, а также могут применять данный метод для ее обучения.
Задействуются функции правдоподобия для каждого используемого класса. В результате, объект при процедуре классификации относится к тому типу, где вероятность максимальна.
Кроме того, используется специальная формула, которая минимизирует потери от ошибок. Данная функция возвращает нужное число для полученных ошибок. Притом сервис позволяет увидеть, сколько мы теряем в среднем на основе условного и байесовского риска, для чего также используются отдельные формулы.
Такие алгоритмы распознавания применяются к задачам различной сферы. Например:
- распознавание лиц, снятых на камеру;
- распознавание отдельных изображений;
- распознавание штрих-кодов, номеров машин, символов;
- распознавание речи;
- классификация документов и т.д.
Помимо этого, используется диагностическая матрица байесовского метода. В зависимости от заурядности признаков, в таблице появляются соответствующие столбцы на «да-нет». Выделение сегментации происходит согласно априорным диагнозам вероятностей. Именно в составлении данной таблицы, заключается процесс обучения мобильным роботом и формирование нейронов.
Само распознавание происходит благодаря принципу правдоподобия, который учитывает статистические свойства заданного вектора. Данное отношение используется также в других методах, например, Неймана-Пирсона, который применяется в случае, если априорная информация отсутствует. Однако именно способ Байеса получил свою популярность, благодаря тому, что в большинстве задач все же получается установить вероятности и потери.
С помощью сервиса пользователи смогут:
- Быстро решить задачу, используя обозначенный подход.
- Достаточно точно выполнить преобразования, даже если требуется распознавать довольно редкие диагнозы. Но в случае необходимости можно провести метод последовательного анализа, чтобы принятие решения было с определенной степенью риска.
В любом случае, обучение роботам необходимо, чтобы гипотезы, проведенные над исходными данными, получили доказательство.
Примеры использования полученной информации
Чтобы пользователям было понятнее, как выглядит сервис, предлагаем ознакомиться с примером работы.
Для начала потребуется загрузить файл в нужном формате:
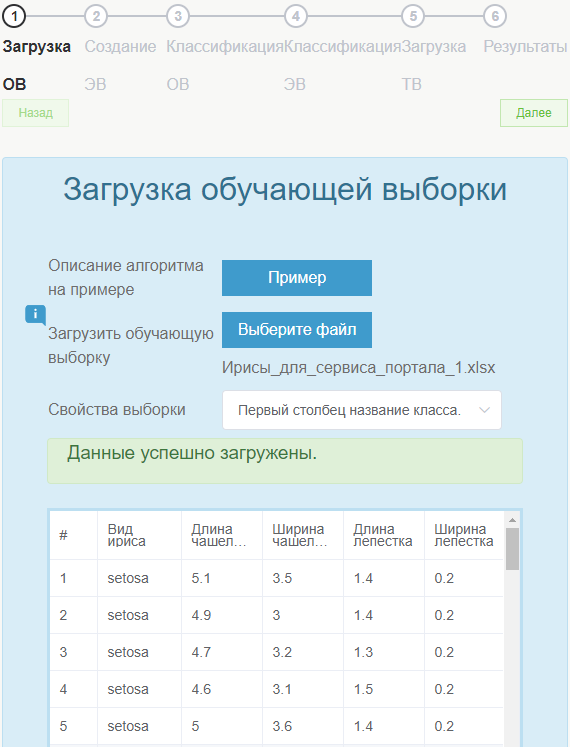
После чего выбирается, какой столбец будет названием класса для последующей выборки.
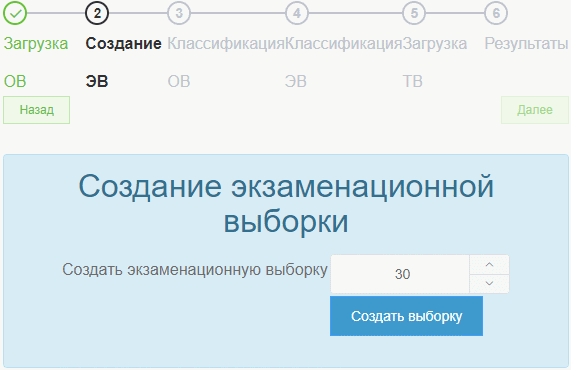
Далее необходимо создать экзаменационную выборку, указав нужное число для исследования.
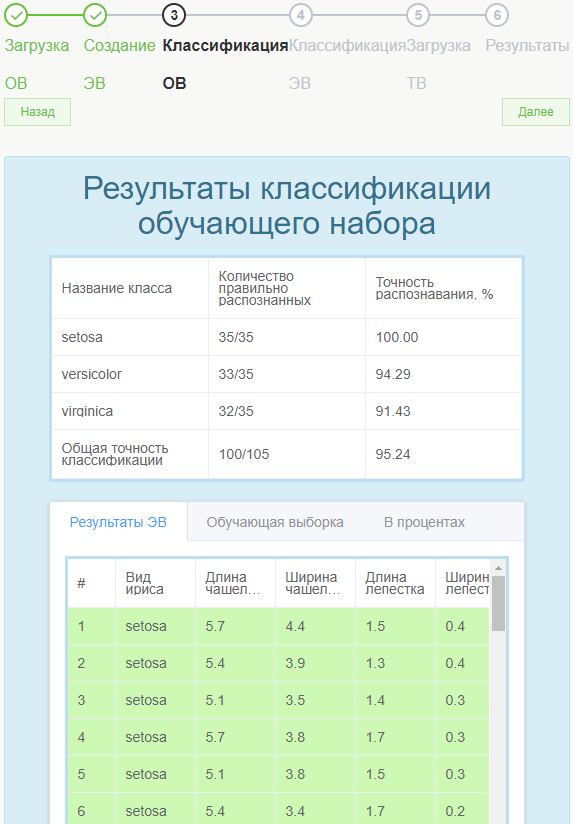
Классификация ОВ позволяет определить точность распознавания в процентном соотношении. Притом, как отдельных признаков, так и общее число классификации.
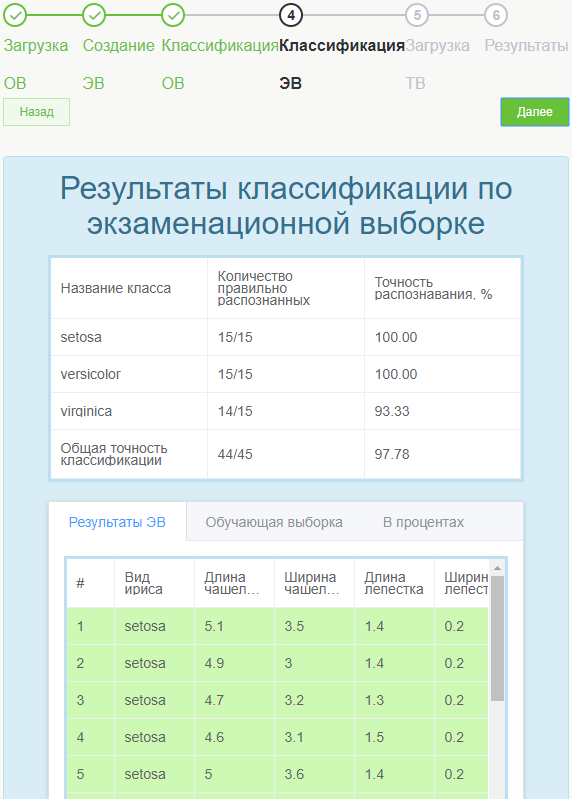
Классификация ЭВ действует по аналогичному принципу, пользователи также видят определение точности данных в процентном соотношении.
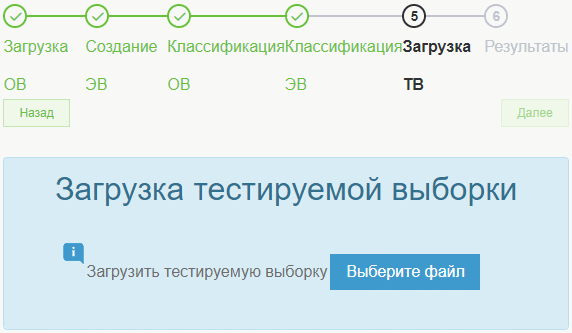
В конце оператору нужно будет загрузить тестируемую выборку, также в нужном формате файла.
После чего можно перейти к результатам работы.