
ScienceHunter Ред. 13.05.2019
Алгоритмы кластеризации
Кластеризация (употребляются также следующие синонимы: автоматическая классификация, кластерный анализ, численная таксономия, алгоритм разбиения на группы, clustering) – объединение в группы схожих объектов – является одной из фундаментальных задач в области анализа данных и Data Mining.
Список прикладных областей, где она применяется, широк: сегментация изображений, маркетинг, борьба с мошенничеством, прогнозирование, анализ текстов. Во всех этих случаях данные, организованы в виде таблицы "объект - свойство" (ТОС).
Таким образом, «объект» в нашем случае – это просто строка в ТОС. Объекты обычно имеют ряд свойств. Столбец в такой таблице – это свойство. Свойствами могут быть признаки, атрибуты, параметры, количественные оценки фондов, показатели развития и другие характеристики, которыми обладают элементы исследуемой совокупности объектов. Выбор (или отбор) свойств для такой ТОС – это отдельная задача, связанная с конкретной предметной областью и решаемая, как правило, с привлечением специалиста в соответствующей области.
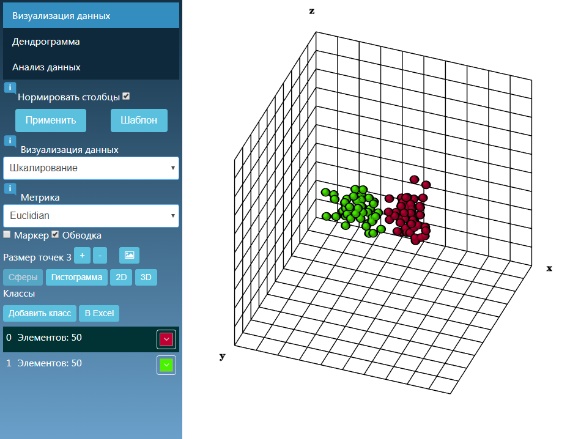
Очень часто кластеризация выступает первым шагом при анализе данных и ее иерархическая важность, несомненно, важна. При этом очень ценным вспомогательным инструментом может служить визуализация, особенно в случае многомерных данных. Такая визуализация позволяет наглядно увидеть группы объектов, которые затем можно объединить в кластеры (cluster), в том числе и визуально. Такой сервис представлен на сайте sciencehunter.net - помогает в проведении кластерного анализа. Для того, чтобы лучше понять порядок действий с этим инструментом (визуализации и кластеризации) ниже доступно видео.
Tutorial для правильного составления документов WORD есть в приложении. Следовать правилам нужно, для распознавания множества классов, успешного проведения алгоритма выборки кластеров и, как следствие - получение логических результатов и визуальной классификации. На основе данных выборки можно разобраться, к какому классу относиться тот или иной объект и проследить особенность каждого кластера.
Заметим, что после выделения схожих групп, в зависимости от целей анализа, могут применяться другие методы, и для каждой группы строится отдельная модель.
Задачу кластеризации в том или ином виде формулировали в таких научных направлениях, как статистика, распознавание образов, оптимизация, машинное обучение (machine learning). Отсюда многообразие синонимов понятию кластер – класс, таксон, сгущение.
На сегодняшний момент число методов разбиения групп объектов на кластеры довольно велико – несколько десятков алгоритмов (algorithms mixture - k-means, spaning tree, hierarchic, EM) и еще больше их модификаций. Однако нас интересуют алгоритмы кластеризации с точки зрения их применения в Data Mining.
Кластеризация в Data Mining приобретает ценность тогда, когда она выступает одним из этапов анализа данных, построения законченного аналитического решения. Аналитику часто легче выделить группы схожих объектов, изучить их особенности и построить для каждой группы отдельную модель, чем создавать одну общую модель на всех данных. Таким приемом постоянно пользуются в маркетинге, выделяя группы клиентов, покупателей, товаров и разрабатывая для каждой из них отдельную стратегию.
Очень часто данные, с которыми сталкивается технология Data Mining, имеют следующие важные особенности:
- высокая размерность (тысячи полей) и большой объем (сотни тысяч и миллионы записей) таблиц баз данных и хранилищ данных (сверхбольшие базы данных);
- наборы данных содержат большое количество числовых и категорийных атрибутов.
Все атрибуты, или признаки объектов делятся на числовые (numerical) и категорийные (categorical). Числовые атрибуты – это такие, которые могут быть упорядочены в пространстве, соответственно категорийные – которое не могут быть упорядочены. Например, атрибут "возраст" – числовой, а "цвет" – категорийный. Приписывание атрибутам значений происходит во время измерений выбранным типом шкалы, а это, вообще говоря, представляет собой отдельную задачу.
Большинство алгоритмов кластеризации предполагают сравнение объектов между собой на основе некоторой меры близости (сходства) или расстояния между объектами. Мерой близости называется величина, имеющая предел и возрастающая с увеличением близости объектов или уменьшающаяся при уменьшении расстояния между объектами. Меры сходства "изобретаются" по специальным правилам, а выбор конкретных мер зависит от задачи, а также от шкалы измерений. В качестве меры близости для числовых атрибутов очень часто используется евклидово расстояние d, вычисляемое по формуле:
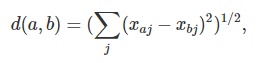 где xaj, xbj – координаты векторов (объектов или строк ТОС) соответственно a и b j = 1,…, P, P – число столбцов в ТОС.
где xaj, xbj – координаты векторов (объектов или строк ТОС) соответственно a и b j = 1,…, P, P – число столбцов в ТОС.
Для получения более подробных сведений Вы можете обратиться к нашему электронному учебнику в раздел Clasterization(Кластеризация), воспользоваться приведенными там иллюстративными примерами, а также решить предложенные там же задачи, задать интересующие Вас по этому разделу вопросы и получить на них ответы.